BGScript Random Number Generator

In the past few months, I’ve done a fair amount of BGScript work for my own projects, as well as for some of my clients. One feature that pops up occasionally is the need to generate a random number. In most programming languages, there is a built-in language-level (or standard library) feature which uses a seeded random number generator (or pseudo-random number generator) to generate a random integer. BGScript did not have this functionality - until now.

Note: The full sample code for this post is on my Github page, in my BLE113 examples repo (https://github.com/sureshjoshi/ble113-firmware-examples).

As per this Bluegiga forum post, you can generate a somewhat random number by using (effectively) noise from the LSBs of the internal temperature sensor. This method works, but what I noticed in practice is that the same numbers are repeated very often, like a bad version of the 80/20 rule (as a ballpark, let’s say we have 1 byte’s worth of random numbers, out of 255 possible values, I saw the same 30 numbers over 75% of the time).

I didn’t dig into this, but I assume it’s partially caused by the quantization levels of the ADC - but it really doesn’t matter.

My PRNG (that’s what people in the biz call pseudo-random number generators) research took me through a lot of random number generator algorithms, but this being BGScript and having all its performance and maintainability limitations - I decided easiest was best. Which brings me to xorshift.

XORshift?

Whenever I see XOR, I immediately picture someone with their hands in their pockets shrugging cluelessly… No idea why…

Anywho, the xorshift wiki page has a fantastically simple C++ algorithm:

#include <stdint.h>

/* These state variables must be initialized so that they are not all zero. */
uint32_t x, y, z, w;

uint32_t xorshift128(void) {
    uint32_t t = x ^ (x << 11);
    x = y; y = z; z = w;
    return w = w ^ (w >> 19) ^ t ^ (t >> 8);
}

So fantastically simple, that it can be written in BGScript identically:

# Perform a xorshift (https://en.wikipedia.org/wiki/Xorshift) to generate a pseudo-random number
export procedure rand()
    t = x ^ (x << 11)
    x = y
    y = z
    z = rand_number
    rand_number = rand_number ^ (rand_number >> 19) ^ t ^ (t >> 8)
end

Can’t spell ‘random number generator’ without ‘seed’

So, that was pretty easy… And there’s only one way to screw the function up… Use default initialization values for x, y, z, and rand_number. The reason is, xorshift makes exclusive use of two operations: XOR and bit-shifts - and doing either of those operations on zeros results in zeros.

The solution is pretty simple. Use ANYTHING except all zeros. Pick your favourite number, pick 1, pick 42, whatever - just not all zeros.

Not a very random number generator

The downside with using a constant number is that each device, on boot, will generate the exact same sequence of ‘random’ numbers. The easy way to fix this is to involve a device-specific value into the seed - in my case, this value is the last 2 digits of the MAC address of the module.

# Get local BT address
call system_address_get()(mac_addr(0:6))
...
tmp(15:1) = (mac_addr(0:1)/$10)+ 48 + ((mac_addr(0:1)/$10)/10*7)
tmp(16:1) = (mac_addr(0:1)&$f) + 48 + ((mac_addr(0:1)&$f )/10*7)
...
# Seed the random number generator using the last digits of the serial number
seed = (tmp(15) << 8) + tmp(16)
call initialize_rand(seed)

Now, we’ve handled the sequencing between devices, but what about if this is a device which is rebooted often? The same device will still generate the exact same sequence of numbers on boot.

Well, this is where that tidbit of information from the Bluegiga forum comes in handy. We can use the device serial number AND add a little bit of randomness with the LSBs of the ADC internal temperature reading to reduce the likelihood of getting the same sequence on consecutive boots (not impossible, not even improbable, just less likely).

    ...
    # Seed the random number generator using the last digits of the serial number
    seed = (tmp(15) << 8) + tmp(16)
    call initialize_rand(seed)

    # For some extra randomness, can seed the rand generator using the ADC results from internal temperature
    call hardware_adc_read(14, 3, 0)
end


event hardware_adc_result(input, value)
    if input = 14 then
        # Use ambient temperature check to augment seed
        seed = seed * (value & $ff)
        call initialize_rand(seed)
    end if
end

See it to believe it

Just to make sure I wasn’t out to lunch, I tested the generator by generating a few thousand numbers and put them on a scatterplot to see if there were any patterns I could notice… I could not… This scatterplot is not a replacement for a thorough mathematical analysis, but for my applications, it really doesn’t matter.

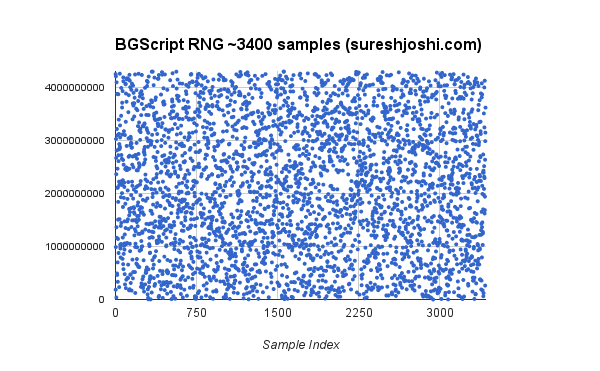
Just as a reminder, the full code for this post can be found here (under Random): https://github.com/sureshjoshi/ble113-firmware-examples

And one last note… I would hope to not need to mention this, but please don’t use something like this for anything dealing with cryptography.

UPDATE (April 29th, 2015):

I’ve found what appears (at first glance) to be a quirk in the rand() system when trying to segment the random numbers into useful buckets (for instance, if 25% of the time I want a 1 to appear).

Here is some sample code for a test I ran, as well as the result. It looks like in the ‘if’ statements, you need to bucket between 0 and 2^31 (rather than either -2^31 to 2^31, or 0 to 2^32). Not sure of the scoop just yet, but this code seems to work (generates certain numbers 25%, 25%, 35%, and 15% of the time)

# Generate a random number and return it to the debugging output
call rand()
if rand_number <= 536870912 then  # 25% of the time
    rand_result = 1
end if

if rand_number > 536870912 && rand_number <= 1073741824 then  # 25% of the time
    rand_result = 2
end if

if rand_number > 1073741824 && rand_number <= 1825361100 then  # 35% of the time
    rand_result = 3
end if

if rand_number > 1825361100 then  # 15% of the time
    rand_result = 4
end if

tmp(0:4) = rand_result
call attributes_write(xgatt_debug, 0, 4, tmp(0:4))

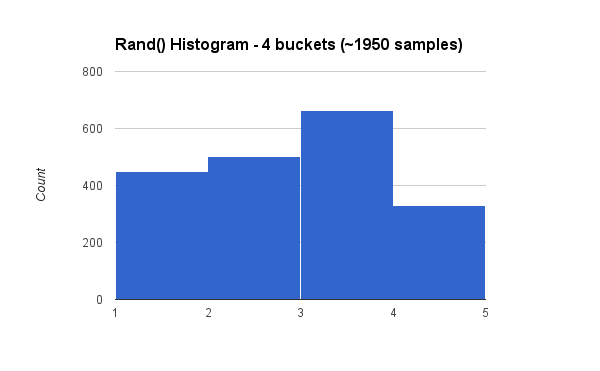
Here is the corresponding histogram across ~1950 samples. I’ve run this test a few times, and the results come out really close to their predicted ratios.

UPDATE (November 13th, 2016):